탐색적 데이터 분석 (EDA, Exploratory Data Analysis)
기존 통계학이 정보 추출에서 가설 검정 등에 치우치다 보니, 자료 본연의 의미를 찾는데 어려움이 존재함.
이를 보완하고자 주어진 자료만 가지고도 충분한 정보를 찾을 수 있도록하는 여러 탐색적 자료 분석 방법.

- 내 입맛대로 수집되는 데이터는 1도 없다
- 데이터의 분포를 파악할 수 있다
- 분석에 필요한 데이터 전처리를 수행할 수 있다
- 데이터의 생김새를 알아야 올바른 분석을 할 수 있다
- 결측치, 이상치를 파악하고 처리할 수 있다
- 가장 적합한 분석 방법을 결정할 수 있다
- 결측: 계획된 실험 배치에서 어떤 사고로 이루어지지 못한 관측
기초 통계량 계산
* 합계=SUM(범위)
* 중앙값=MEDIAN(범위). 자료를 크기 순서로 나열해 놓았을 때 위치적으로 중앙에 있는 값
ex) 1,2,3,4,5 : 중앙인 3번째의 3 // 1,2,3,4,5,6 : 절대적인 중앙값이 없으므로 중앙에 위치한 두 값의 평균, (3+4)/2=3.5
* 최대값=MAX(범위)
* 최솟값=MIN(범위)
* 평균=AVERAGE(범위)
* 최빈값=MODE(범위), 가장 많이 등장하는. 빈도수 높은 값
ex) 1,2,2,3,3,3,2,1의 최빈값 : 2, 3
* 분산=VAR(범위), 평균을 기준으로 데이터가 흩어져있는 정도.
분산이 높으면 각 값들이 평균과 차이가 많이 남 / 분산이 낮으면 각 값들이 평균과 비슷한 값들임
* 표준편차=STDEV(범위) , 분산의 제곱근(표준편차의 제곱=분산)
피벗 테이블 활용
커다란 표의 데이터를 요약하는 통계표

어려운 이유?
어떤 요약 통계표를 만들어야 하는지 명확하지 않기 때문
* 피벗 테이블 생성
Raw data 선택 > [삽입] 탭 > 피벗 테이블

피벗 테이블 사용하기
[피벗 테이블 필드]의 필드를 필터/열/행/값 중 필요한 부분에 드래그

Boxplot & 산점도
* Boxplot
최솟값, 제1사분위수, 중앙값, 제3사분위수, 최댓값을 활용해 그리는 그래프
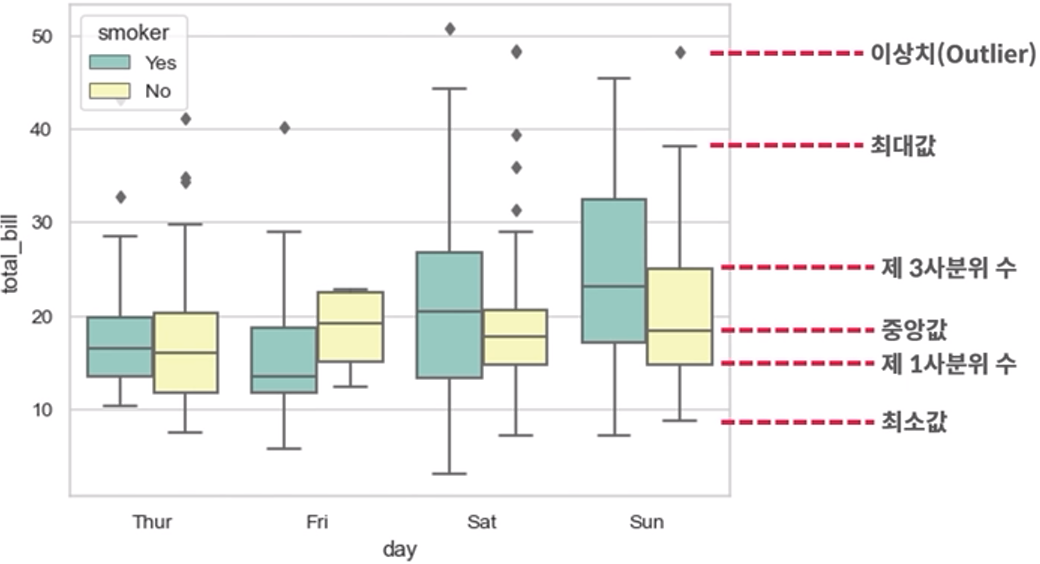
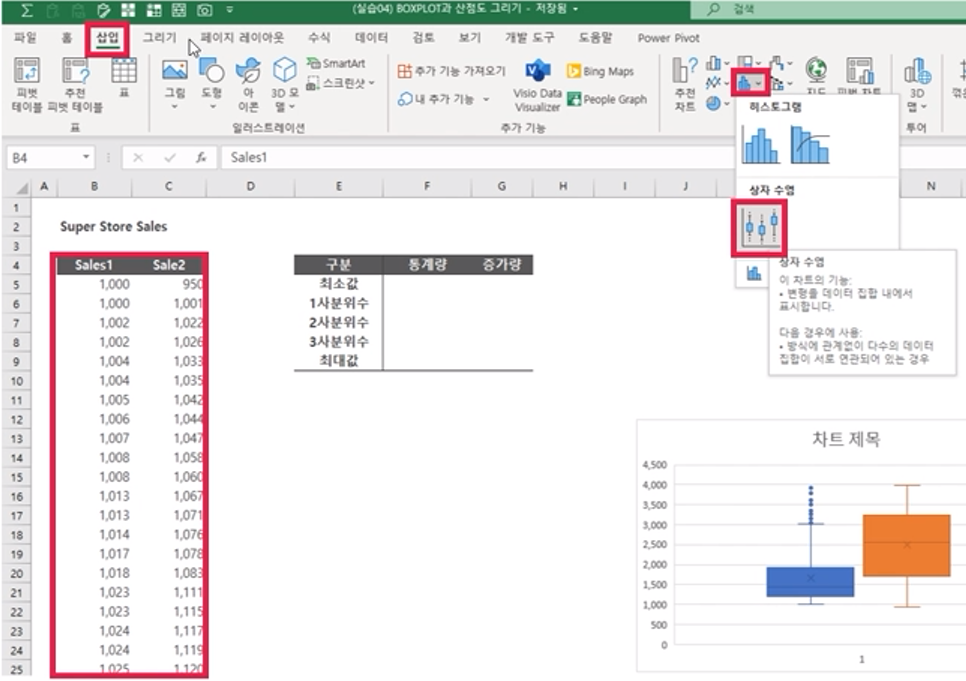
최소값/사분위수/최댓값 구하기 (엑셀 2013이하 에선 최소값, 1,3사분위수, 최대값 등을 미리 구해놓고 차트를 만들어야)
=QUARTILE(범위, 데이터 종류 지정)
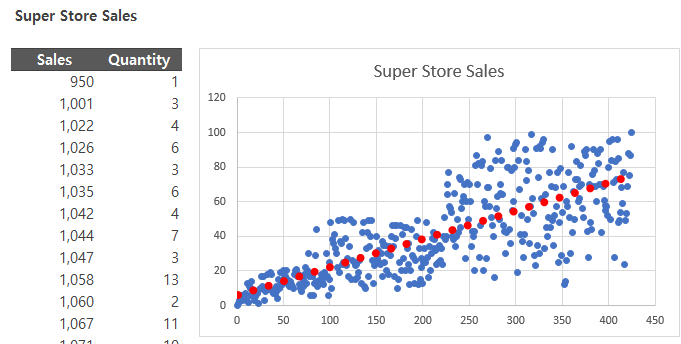
* 산점도
데이터를 점으로 표현해 흩어져 있는 정도를 파악하는 그래프
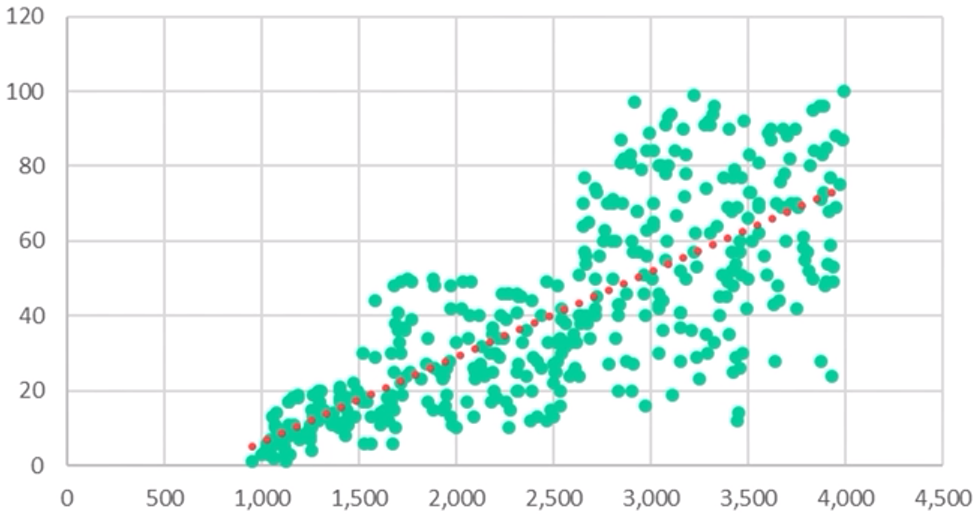
[삽입] > 차트의 분산형(X, Y) 또는 거품형 차트 삽입에서 선택 > 분산형 선택
빈 차트가 나오면 > 데이터 선택해서 보여줄 정보 표시
X , Y 축에 표시할 정보를 선택한다
* 추세선 표시하기
차트에서 마우스 오른쪽 버튼 > 추세선 추가
'온라인 강의 내용 > 패캠-데이터분석' 카테고리의 다른 글
| 4. 데이터분석과 엑셀 : MATCH, INDEX, 날짜함수, 텍스트함수, 텍스트나누기, 중복항목 제거 (0) | 2023.09.10 |
|---|---|
| 3. 데이터분석과 엑셀 : 데이터 전처리 , IF, VLOOKUP (0) | 2023.08.27 |
| 1. 데이터분석과 엑셀 : 데이터 분석 개념 , 엑셀의 참조 (0) | 2023.08.16 |


